Sådan konverteres fra binær til decimal

Den binære (base to) talsystem har to mulige værdier, ofte repræsenteret som 0 eller 1, for hvert sted-værdi. I modsætning hertil decimal har (base ti) talsystem ti mulige værdier (0,1,2,3,4,5,6,7,8, eller 9) for hvert sted-værdi.

For at undgå forvirring, mens du bruger forskellige numeriske-systemer, bunden kan i hvert enkelt nummer angives ved at skrive det som en sænket af nummeret. For eksempel kan det binære tal 10011100 angives som "base to" ved at skrive det som 10011100 _2. Det decimaltal 156 kan skrives som 156 ₁₀ og læses som "156, bund ti".

Da det binære system er den interne sprog i elektroniske computere, bør alvorlige edb-programmører at forstå, hvordan man konverterer fra binær til decimal. Konvertering i den modsatte retning, fra decimal til binær, er ofte sværere at lære først.

Bemærk: Dette er KUN for optælling og taler ikke om ASCII oversættelser.

Steps

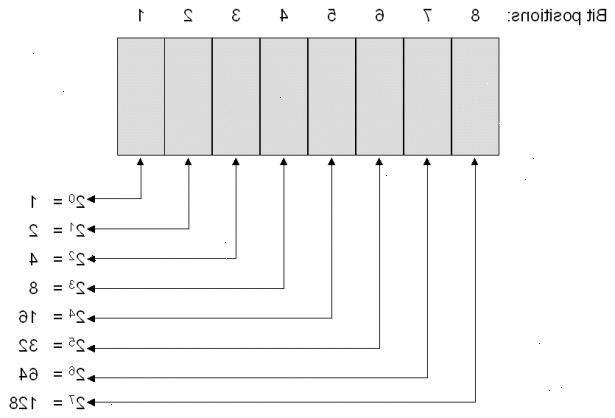
Sådan konverteres fra binær til decimal. Skriv først det binære tal under listen.

Positional notation metode

1
For dette eksempel, lad os konvertere det binære tal 10011011 ₂ til decimal. Anfør de beføjelser to fra højre til venstre. Start ved 2 ^0, evaluere det som 1. Øg eksponent med én for hver strøm. Stop, når mængden af elementerne på listen er lig med mængden af cifre i det binære tal. Eksemplet nummer 10011011, har otte cifre, så listen, til otte elementer, ville se sådan ud: 128, 64, 32, 16, 8, 4, 2, 1
2
Skriv først det binære tal under listen.
3
Tegne linjer, startende fra højre, der forbinder hver efterfølgende ciffer i binære tal til magten af to, der er næste på listen over det. Begynd ved at tegne en linje fra det første ciffer i det binære tal til den første strøm af to på listen over det. Derefter trækker en linje fra det andet ciffer i det binære tal til den anden magt to på listen. Fortsæt forbinder hvert ciffer med dens tilsvarende potens af to.
4
Flyt gennem hvert ciffer i binære tal. Hvis det ciffer er et 1, skrive sin tilsvarende potens af to under linien, under det ciffer. Hvis det ciffer er et 0, skriv en 0 under linjen under det ciffer.
5
Tilføj numrene skrevet under linien. Summen skal være 155. Dette er den tilsvarende decimaltal af binære tal 10011011. Eller skrevet med basis sænket:
6
Gentagelse af denne metode vil resultere i udenadslære af de beføjelser, af to, som vil give dig mulighed for at springe trin 1.

Fordobling metode

1
Denne metode bruger ikke kræfter. Som sådan er det enklere for at konvertere et stort antal i dit hoved, fordi du kun behøver at holde styr på en subtotal.
2
Start med den længst til venstre ciffer i givet binære tal. For hvert ciffer som du flytter til højre, fordoble din tidligere total og tilføje den aktuelle ciffer. For eksempel for at konvertere 1011001 ₂ til decimal, vi tage følgende skridt:
3
1011001 → 0 * 2 + 1 = 1
4
1011001 → 1 * 2 + 0 = 2
5
1011001 → 2 * 2 + 1 = 5
6
1011001 → 5 * 2 + 1 = 11
7
1011001 → 11 * 2 + 0 = 22
8
1011001 → 22 * 2 + 0 = 44
9
1011001 → 44 * 2 + 1 = 89 ₁₀
10
Ligesom den positionelle notation metode, kan denne fremgangsmåde modificeres konverteres fra hvilken som helst base til decimal. Fordobling bliver brugt, fordi det angivne antal er base 2. Hvis det angivne antal er af en anden base, erstatte 2 i fremgangsmåden med bunden af et givet tal. For eksempel, hvis det angivne antal er i bunden 37 vil du udskifter * 2 med * 37.. Det endelige resultat vil altid være i decimal (base 10).

Tips

Praksis. Prøv at konvertere det binære tal 11010001 _2, 11001 ₂ og 11.110.001 _2.. Henholdsvis deres decimale ækvivalenter 209 _10, 25 ₁₀ og 241 _10.
Regnemaskinen der kommer installeret med Microsoft Windows kan gøre denne konvertering for dig, men som programmør, er du bedre tjent med en god forståelse af, hvordan konverteringen virker. Den lommeregnerens konverteringsmuligheder kan gøres synlige ved at åbne sin menuen "Vis" og vælge "videnskabelige". På Linux kan du bruge galculator.

Advarsler

Dette bruger binære, snarere end signeret, decimaltal eller.